El teorema de Pitágoras puede ser considerado como el teorema más importante de la geometría. Este teorema nos permite utilizar una ecuación algebraica para resolver problemas geométricos. De acuerdo con el teorema de Pitágoras, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Recordemos que la hipotenusa es el lado opuesto al ángulo recto en un triángulo rectángulo y los catetos son los otros dos lados del triángulo.
A continuación, conoceremos un poco de historia de este teorema. Además, aprenderemos cómo demostrarlo y lo usaremos para resolver algunos ejercicios de práctica.
Historia del teorema de Pitágoras
Pitágoras de Samos (569-500 a. C.) nació en la isla de Samos en Grecia y viajó mucho por Egipto, aprendiendo matemáticas y otras cosas. Se desconocen más detalles sobre cómo fueron sus primeros años. Pitágoras empezó a ser reconocido y a formarse un estatus al fundar un grupo conocido como la Hermandad de Pitágoras, que tenía como objetivo al estudio de las matemáticas.
La hermandad de Pitágoras tenía varios aspectos de un culto como por ejemplo, símbolos, rituales y oraciones. Además, Pitágoras creía que «el número gobierna el universo», y los miembros del grupo de Pitágoras dieron valores numéricos a muchos objetos e ideas. Estos valores numéricos, a su vez, estaban dotados de cualidades místicas y espirituales.
Una leyenda cuenta que cuando Pitágoras termino su famoso teorema, él sacrificó 100 bueyes. A pesar de que este teorema es atribuido a Pitágoras, no es posible conocer con certeza si es que él fue verdaderamente el autor real. El grupo de la Hermandad de Pitágoras trabajó en muchas pruebas geométricas, pero es difícil saber quién probó qué, ya que el grupo siempre trató de mantener en secreto sus hallazgos.
Desafortunadamente, este voto de secreto evitó que se conociera públicamente sobre una idea matemática importante. La Hermandad de Pitágoras había descubierto los números irracionales. Cuando consideramos a un triángulo rectángulo isósceles con catetos de medida 1, la hipotenusa medirá la raíz cuadrada 2.
Sin embargo, sabemos que este número no puede ser expresado como una longitud que se puede medir con partes fraccionarias, y eso perturbó profundamente a los pitagóricos, que creían que «Todo es número».
Fórmula del teorema de Pitágoras
El teorema de Pitágoras indica que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Por ejemplo, en el siguiente triángulo rectángulo, la hipotenusa es el lado c y los catetos son los lados a y b.
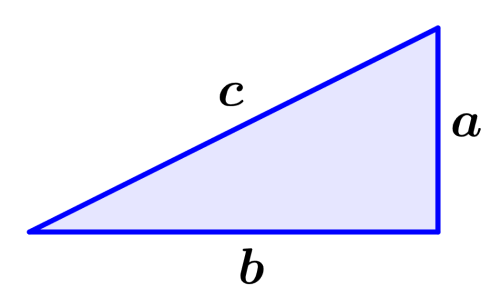
Entonces, por el teorema de Pitágoras, tenemos:
Esta fórmula nos permite encontrar la longitud de la hipotenusa si es que conocemos la longitud de los dos catetos. Alternativamente, podemos usar la fórmula para encontrar la longitud de uno de los catetos si es que conocemos la longitud de la hipotenusa y el otro cateto.
Demostraciones del teorema de Pitágoras
Existen varios métodos que pueden ser usados para demostrar el teorema de Pitágoras. Sin embargo, los más comunes son la demostración de Pitágoras y la demostración a través del álgebra.
Demostración de Pitágoras
Podemos empezar con el siguiente triángulo rectángulo:

Las longitudes a y b representan a los catetos y la longitud c representa a la hipotenusa. Usando cuatro de estos triángulos, vamos a formar un cuadrado grande con lados de longitud :
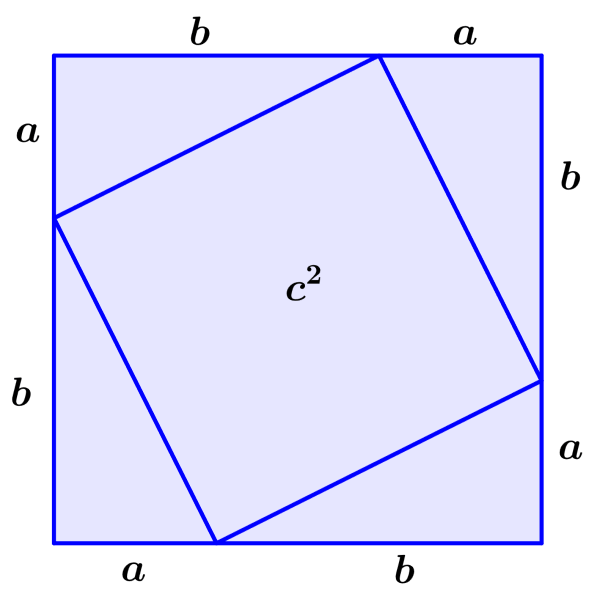
Los lados del cuadrado interno tienen una longitud de c ya que son iguales a las hipotenusas de los triángulos. Esto significa que su área es igual a .
Vamos a reorganizar a los triángulos de la siguiente manera:
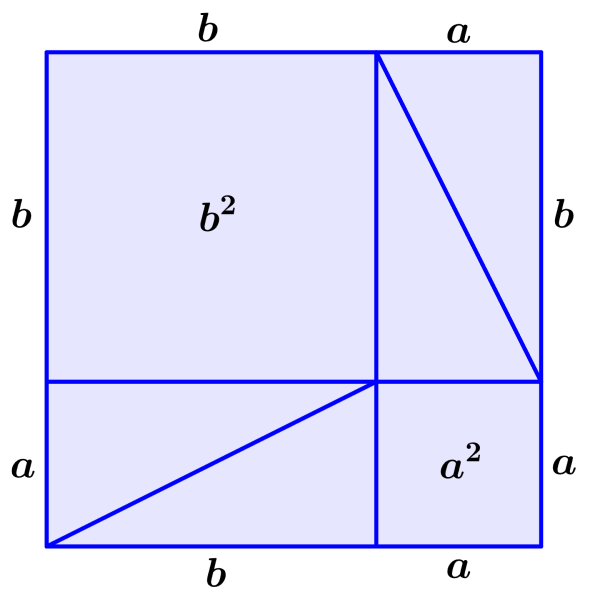
Esto forma a dos cuadrados con las áreas y
.
El área de ambos cuadrado grandes formados es la misma en ambos casos. Dado que los triángulos usados son los mismos, el área de los cuadrados y
es igual al área del cuadrado
. Es decir, tenemos:
Demostración usando álgebra
Podemos usar un diagrama similar al que usamos anteriormente. Cuatro triángulos rectángulos son usados para formar un cuadrado grande y un cuadrado interno con lados iguales a las hipotenusas de los triángulos.
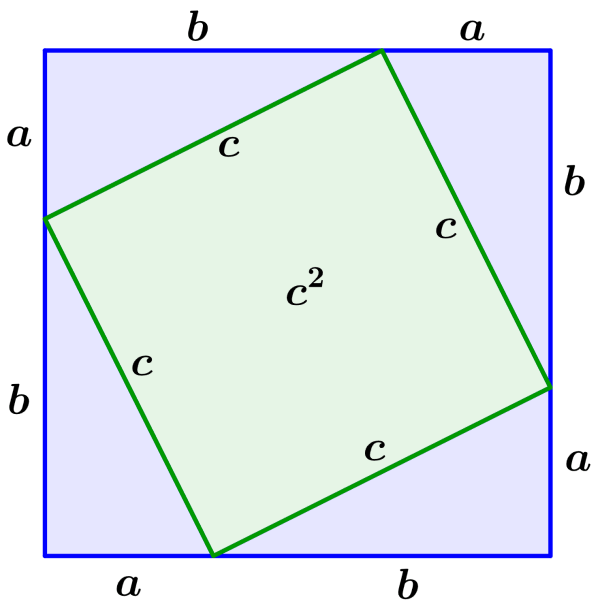
Las longitudes a y b son los catetos de los triángulos y c es la hipotenusa. El cuadrado grande formado tiene lados de longitud . Esto significa que su área es igual a
Dado que el cuadrado interno tiene lados de c, su área es igual a . Adicionalmente, podemos observar que el área del cuadrado grande es igual al área de los cuatro triángulos más el área del cuadrado interno. Esto significa que tenemos:
Ejemplos de aplicación del teorema de Pitágoras
Los siguientes son algunos ejemplos de cómo resolver problemas con el teorema de Pitágoras.
EJEMPLO 1Si es que tenemos el siguiente triángulo rectángulo, ¿cuál es el valor de X?
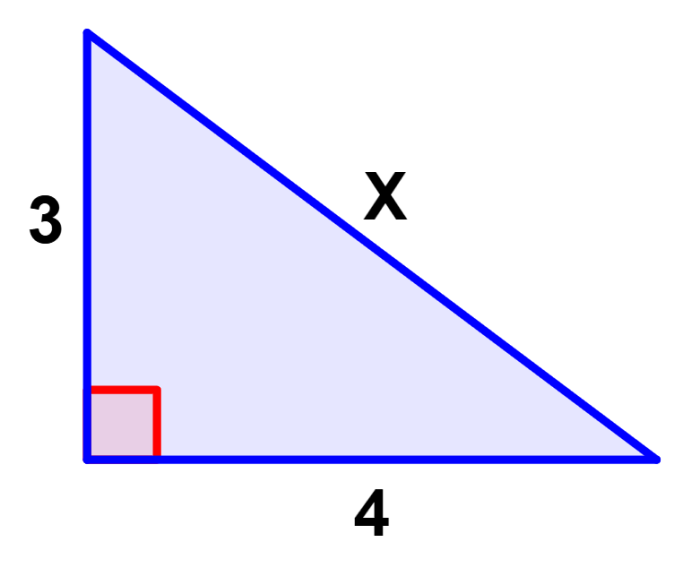
Solución: En este triángulo, 3 y 4 representan a los catetos y X representa a la hipotenusa. Entonces, usando el teorema de Pitágoras, tenemos:
El valor de X es igual a 5.
EJEMPLO 2
Encuentra el valor de Y en el siguiente triángulo rectángulo.
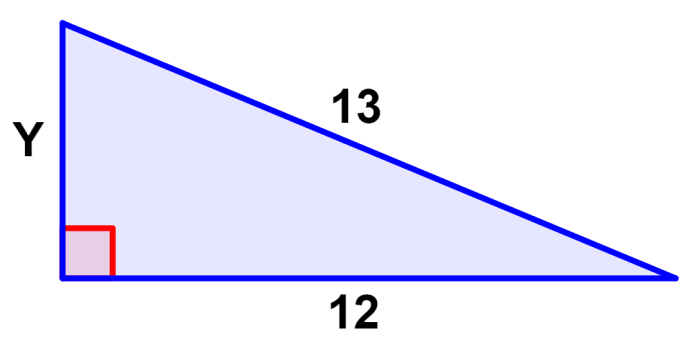
Solución: En este caso, tenemos que encontrar el valor de uno de los catetos del triángulo. Entonces, tenemos que usar el teorema de Pitágoras y resolver para a o para b:
El valor de Y es 5.
EJEMPLO 3
Un triángulo rectángulo tiene una hipotenusa de 13 m y un cateto de 9 m. ¿Cuál es la longitud del otro cateto?
Solución: Podemos reconocer los valores c=13 y a=9. Entonces, simplemente usamos el teorema de Pitágoras con estos valores y resolvemos para b que corresponde al valor del otro cateto:
La longitud del otro cateto es igual a 9.38 m.
EJEMPLO 4
Si es que el cuadrado de la hipotenusa de un triángulo rectángulo isósceles es igual a 128 m². ¿Cuál es la longitud de uno de los catetos?
Solución: Recordemos que un triángulo rectángulo isósceles es un triángulo que tiene un ángulo recto y que tiene dos catetos con la misma longitud. El siguiente es un diagrama de este triángulo:
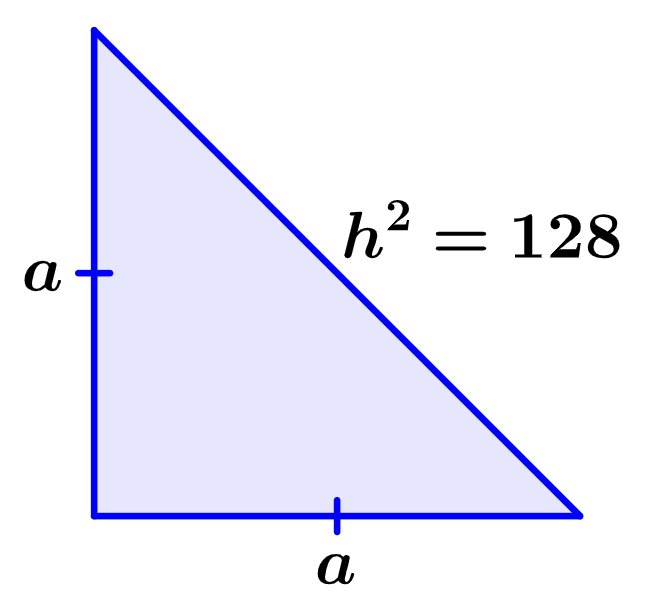
Entonces, al aplicar el teorema de Pitágoras con este triángulo, tenemos lo siguiente:
La longitud de uno de los catetos es igual a 8 m.
Fuente: https://www.neurochispas.com/


